깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 정리 - 기본적인 특징과 유의 사항에 대해서

깊이 우선 탐색과 너비 우선 탐색에 대해 간단하게 비교하여 정리하고자 한다.

두 알고리즘은 생각보다 알고리즘 문제 풀이에서 많이 볼 수 있고, 각각의 응용 방식을 통해 나오는 코딩 테스트 문제가 많기 때문에 참고해두는 것이 좋고, 기본적인 구현 방식은 알고 접근하는 것이 좋다. 기본적인 구현 코드는 백준 온라인 저지의 1260번 DFS와 BFS 을 구현하는 코드이다.

 

DFS, BFS

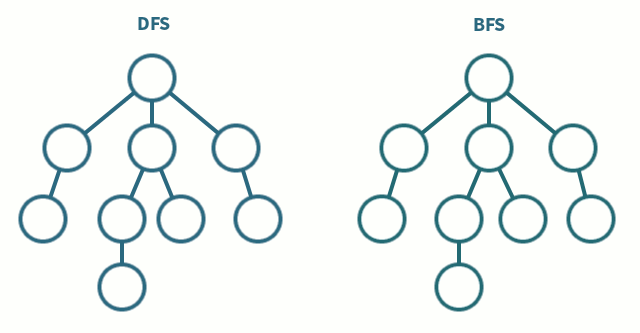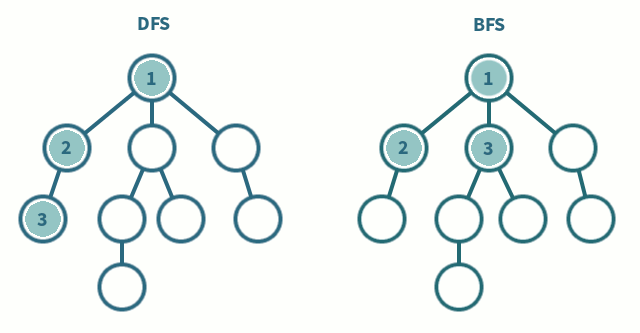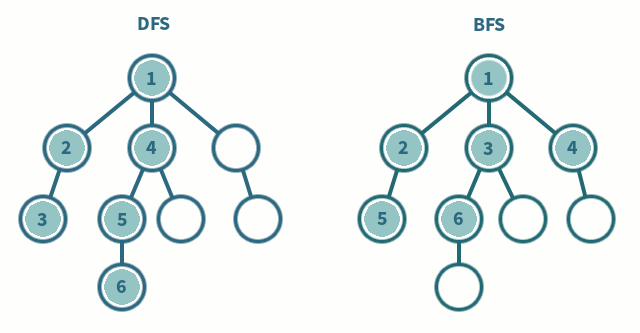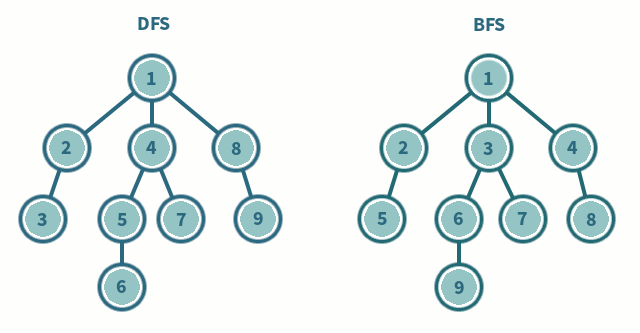
DFS(Depth-First Search)

Stack으로 구현할 수 있고, 함수 호출도 Stack처럼 이뤄지기 때문에 대부분 재귀 함수로 구현된 코드들이 많다. DFS는 미로 찾기로 치면, 막히는 곳까지 계속 파고 드는 Leaf-wise한 방식이다. 분기점이 나오면 길 하나를 선택하고 더 이상 진행하지 못하는 시점까지 진행한다고 보면 이해하기가 쉽다. 위에 보이는 예시처럼 일단 파고들기 시작하면 말단 노드까지 직진하는 방식이다.

 

 

Stack

void DFSStack(int num)
{
	stack<int> st;

	for (int i = 0; i <= n; i++)
		visit[i] = false;

	st.push(num);
	while (!st.empty())
	{
		int cur = st.top();
		st.pop();
		if (!visit[cur])
		{
			cout << cur << " ";
			visit[cur] = true;
			for (int i = n; i >= 1; i--)
			{
				if (cur == i)
					continue;
				if (graph[cur][i] && !visit[i])
					st.push(i);
			}
		}		
	}
}

 

 

Recursive

void DFS(int num)
{
	cout << num << ' ';
	for (int i = 1; i <= n; i++)
		if (graph[num][i] && !visit[i])
			visit[i] = 1, DFS(i);
}

 

특이사항

1. 경로 상 노드를 모두 기억해, 적은 메모리를 사용한다.
2. 찾는 노드가 깊은 곳에 있을 때는 BFS보다 빠르다.
3. 해가 없는 상황에서, 단계가 끝날 때까지 탐색하며 이 과정에서 탐색 깊이를 지정하여 무의미한 탐색을 회피할 수 있다.
4. 해를 탐색하면 종료되기 때문에, 얻어진 해가 최단 경로라는 보장이 없다.

 

 

BFS(Breadth-First Search)

Queue로 구현할 수 있다. BFS는 미로 찾기로 치면, 야금야금 넓게 보는 방식이다. 말이 너무 추상적이라 이해하기 어려울 수 있는데, 어느 한 방향을 잡고 막 파고드는 것이 아니라 탐색 가능한 모든 방향을 한 단계씩 진행하는 Level-wise 방식이다. 위 예시에서 보면 알 수 있듯이, 트리에서 같은 레벨에 있는 모든 노드를 탐색하고 나서 다음 노드로 진행하는 방식이다.

 

 

void BFS(int start)
{
	queue<int> q;

	for (int i = 0; i <= n; i++)
		visit[i] = false;

	q.push(start);
	visit[start] = true;

	while (!q.empty())
	{
		int num = q.front();
		q.pop();

		cout << num << ' ';
		for (int i = 1; i <= n; i++)
			if (graph[num][i] && !visit[i])
				visit[i] = true, q.push(i);
	}
}

 

사람마다 다 다른데, 필자는 DFS 구현은 재귀로 하는 게 편했고, BFS 구현이 DFS 구현보다 편하다. 둘이 같이 활용될 수 있는 문제라면, 자신이 편한 것을 활용하면 되지만, 특정 몇몇의 경우에 있어서 둘 중 하나를 선택해야 하는 경우가 존재한다.

 

 

특이 사항

1. 답이 되는 경로가 여럿일 때에도 최단 경로를 보장한다.
2. 최단 경로가 존재하는 것이 보장되면 깊이와 무관하게 답을 찾아낼 수 있다.
3. 경로가 매우 많아질 경우, 많은 메모리가 필요하다.
4. 해가 존재하지 않을 때, 유한 그래프(Finite Graph)에서는 모든 그래프를 탐색한 후 종료 되며, 무한 그래프(Infinite Graph)에서는 탐색도 실패하고, 종료되지도 않는다.

 

유의 사항

방문 여부 체크

두 탐색 모두 방문 여부를 체크하지 않으면 무한하게 탐색하는 문제가 발생할 수 있다.

 

인접 행렬과 인접 리스트

구현 자체는 인접 행렬이 상대적으로 쉽다. 하지만, 활용하는 그래프의 노드의 개수가 많아지는 경우 인접 행렬로 DFS, BFS를 구현하기보다 인접 리스트를 사용하는 것이 좋다. 인접 행렬로 그래프를 구현하는 경우 정점(V)의 수가 많아질 때, O(V^2)라는 공간 복잡도가 문제가 될 수 있어, O(V+E)인 인접 리스트를 활용하는 것이 좋다.

 

활용하는 경우

그래프 모든 곳을 탐색하는 경우, 별 다른 제약 사항이나 어떤 특정 동작이 있는 경우가 아니면, DFS나 BFS 중 구현이 편한 걸 선택해도 무방하다. 하지만, 전처리 과정이 필요하거나 이동에 제약이 있는 경우, 백트래킹 같이 특정 알고리즘을 사용할 때는 DFS를 사용해야 하고, 가중치(weight) 없는 그래프의 최단 경로 문제는 BFS로 접근해야 한다. 이외에도 여러 가지 경우에 대해 DFS나 BFS를 선택해 활용할 때, 적절한 처리를 해줘야 한다.

 

 

 

 

 

[Reference]

https://stackoverflow.com/questions/3332947/when-is-it-practical-to-use-depth-first-search-dfs-vs-breadth-first-search-bf

http://blog.hackerearth.com/wp-content/uploads/2015/05/dfsbfs_animation_final.gifALGORITHMC++BFSDFS

https://stackoverflow.com/questions/3332947/when-is-it-practical-to-use-depth-first-search-dfs-vs-breadth-first-search-bf